Excel PAYMENT: Calculate loan payments easily

Key information

The function PAY in Excel allows us to obtain the periodic payment that we must make for a loan, providing the interest rate (“rate”), the number of payments to be made (“number of periods”) and the total value for which we obtained the loan today ("current value"). In addition, we can tell you how much of the loan we want to have left at the end of the payment (“final value”) and whether payments are made at the beginning or end of the period (“type”).

The basics

• Purpose: PAY It allows us to obtain the periodic payments that we must make for a loan, given the characteristics of the loan.
• Characteristics: The function uses different concepts of financial mathematics to calculate the total periodic payments of the loan, including both interest and the loan itself. For a further review of how loans and similar functions work, you can see the following article.
• Syntax:

=PAYMENT(rate; nper; goes; [vf]; [guy])

• Arguments:

rate = The interest rate used on the loan.

nper = The number of payments that the loan has.

va = The present value (or total value) of all of the loan payments.

vf = Optional. The future value or balance that we want to remain after making the last payment. If the argument is omitted, the PAYMENT function will assume it is 0, meaning the loan will be paid in full.

type = Optional. Indicates when payments are due. If I use the number 0 I will tell the PAYMENT function that payments are due at the end of the period. If I use number 1 I will indicate that payments are due at the beginning. If the argument is omitted the function will assume that they expire at the end (0).

Step 1: Selecting the interest rate for the PAYMENT function in Excel

The first thing to do when calculating a loan payment in Excel is to define the interest rate that we are going to use. This just means telling the function PAY the rate to use, but we must have a couple of considerations.

One of these considerations is to pay attention to the format in which we deliver the information. This means that for the PAYMENT function a rate of 5 is not the same as a rate of 5%. In the following example we have a loan for $100,000, with a rate of 5% and that is paid in 36 periods:

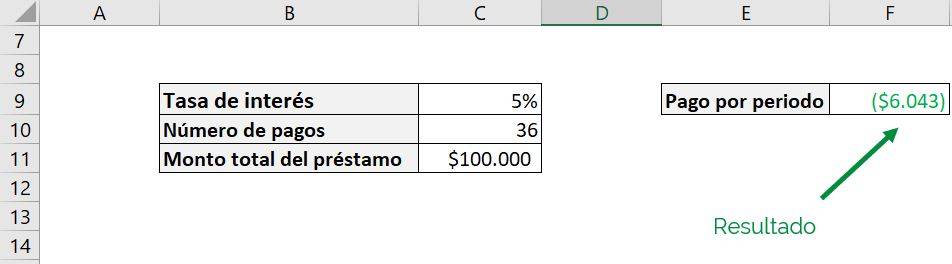
We can see that we get a payment per period of $6,043. This is negative because it is a payment made by us to return the amount of $100,000 that was lent to us.

 However, if we now take out the “%”:

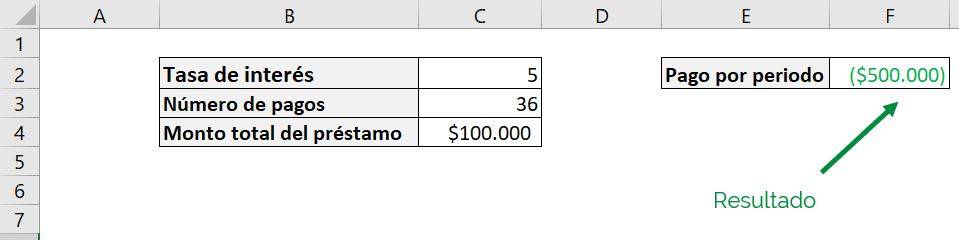
In this case, the PAYMENT function gives us a payment of $500,000 as a result, five times the original loan for each payment! This is because the function is reading the interest rate as 500% instead of 5% as we wanted.

If we wanted to not include the “%” we have to set the rate as 0.05:

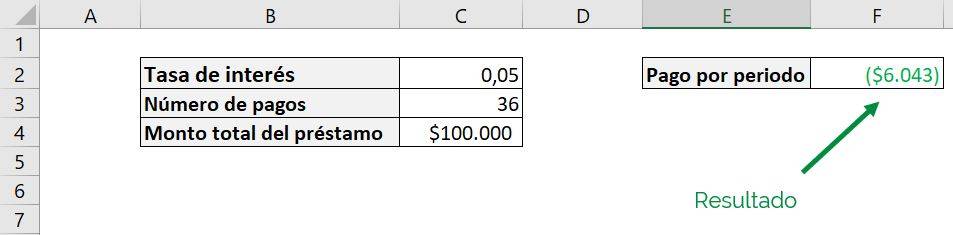
We see that now we obtain the same result as in the first case.

The other issue to consider when using the payment formula in Excel is that the interest rate must match the payment period. That is, if payments are made monthly, the rate must also be monthly. This means that we cannot include an annual fee on a loan that is paid monthly, since Excel would overestimate the amount we must pay each period.

For example, if we want to transform an interest rate from annual to monthly, we must apply the following formula:

(1+Annual rate) ^ (1/12)-1

Which corresponds to applying the root of twelfth (1/12), for the 12 months in a year:

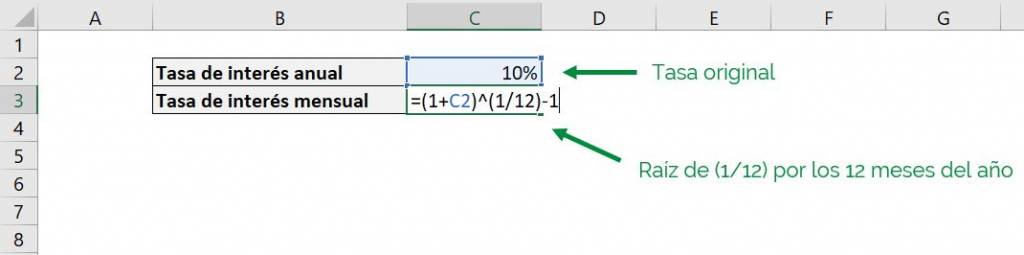
Which gives us the following result:

Tip Ninja: If we want to convert the rate to another type of period, such as semiannual or quarterly, we only have to change the number for which we are applying root. For example, if we want to go from annual to quarterly we must use a 4, since there are 4 quarters in a year.

Ninja Tip: If we want to convert the rate to a longer period type, we must perform the inverse procedure to the previous tip, raising instead of applying root. For example, if we want to go from quarterly to annual we must raise it to 4, for the 4 quarters of the year.

Step 2: Selecting the number of payments for the PAYMENT function

The next step is to indicate the number of payments to our Excel function PAYMENT, which would correspond to the argument nper. In the same way as in step 1, this is only indicating to the function the number of payments that were established in the conditions of the loan, either by writing it in the same function or by indicating the cell where the number appears. But it is also good to have a couple of considerations.

The first consideration is that we must differentiate the time it will take to pay a loan with the number of times a payment must be made. For example, a 10-year loan can have different payment schedules (annual, semi-annual, monthly, etc.), which means that I have to adjust how many payments I am making, since the number of periods is different.

Continuing with the example, let's assume that this loan has a quarterly payment. A possible way to adjust the number of payments is as follows:

In this way, the PAYMENT function will understand that the relevant number for the formula is 40 periods, which is the same as saying that the loan has 40 payments (every quarter).

Step 3: Selecting the current value for the PAYMENT function

The last of the required steps of the PAYMENT function is to select the current loan value. This means the value of the loan today, the money that I am receiving (or giving) in exchange for future payments in installments.

Now that we have our required arguments, we can use them to calculate each payment using our PAYMENT function. In the following example we have a 10-year loan for $100,000, with semiannual payments at an interest rate of 5% simple annual:

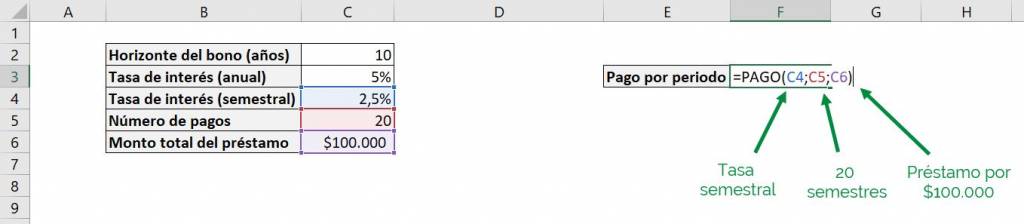
Our arguments are the following:

• rate = C4 (semi-annual rate of 2.5%)
• nper = C5 (20, 10 years with semi-annual payments)
• goes = C6 ($100,000, what the loan is worth today)

Using the PAYMENT function in Excel we obtain the following:

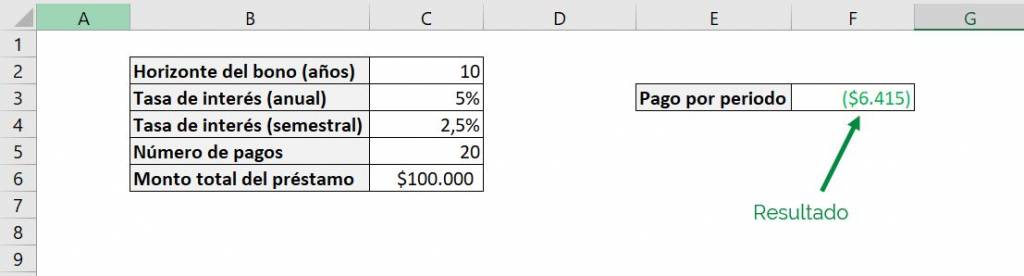
This means that to replace our loan in 10 years we must pay $6,415 semiannually.

Ninja Tip:  You can use Excel function GOES to obtain the current value of a loan using the rate, number of payments and payment per period. This means that you can use this function to check that you are using the PAYMENT function correctly, since using the result obtained you should obtain the original loan amount.

Step 4: Selecting the future value for the PAYMENT function

The first of the optional arguments we have when using the PAYMENT function in Excel is to indicate a future value. This is the balance that will remain after making the corresponding payments. For example, if we want to pay only $30,000 of our $100,000 loan, we indicate to the PAYMENT function that the future value is -$70,000:

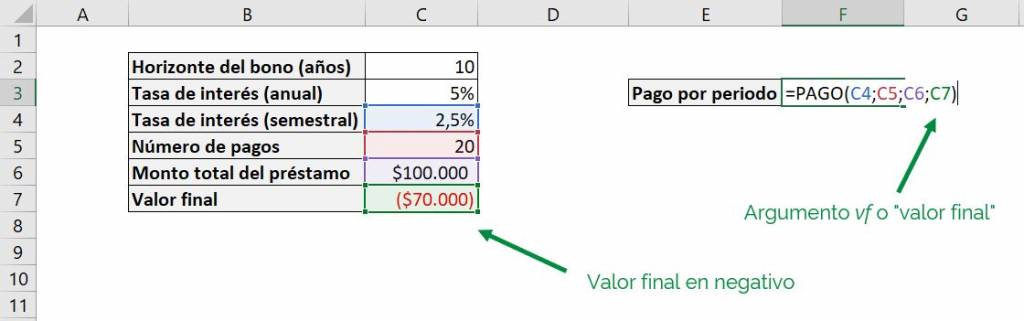
The future value is set to negative in the PAYMENT function because, like the payment that must be made periodically, the function interprets it as an amount of money that is owed to another person. In easy terms, consider that it is money that must come out of the pocket of whoever is calculating the function, and therefore it is being subtracted from the person's wealth. In this case they give me $100,000 at the beginning and I only pay $30,000, so I return the remaining $70,000. This gives us the following results:

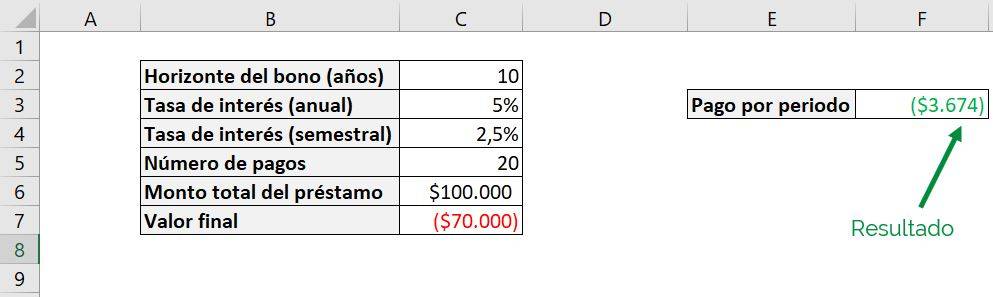
As we can see, the amount we pay per period decreases compared to the case in which we pay the full loan, since we must return less money.

If we now want to use the PAYMENT function to see how much it would cost to pay the entire loan, we just have to replace the final value with 0:

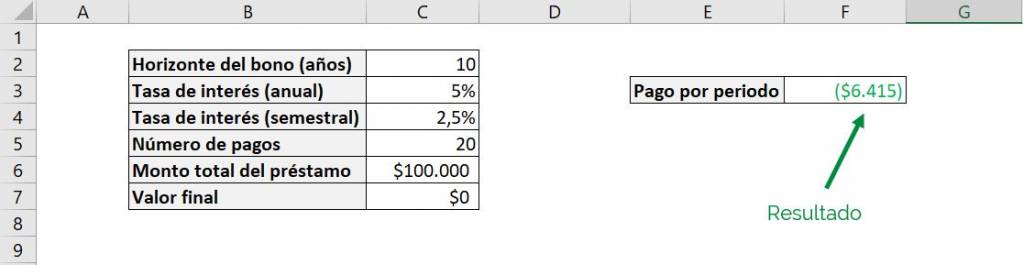
We see that we obtain the same installment as in the example in Step 3, which confirms that the PAYMENT function assumes that the entire loan is paid when we omit the argument vf.

Step 5: Selecting when to pay in the PAYMENT function

The second of the optional arguments that we have when using the PAYMENT function in Excel is to indicate when the loan payments are made. Here we have 2 options:

• Tell the function that payments are made at the end of the period. For example, if they are semiannual payments, they would be June 30 and December 31. In this case we use a “0”. This is the default option in case the argument is omitted guy.
• Tell the function that payments are made at the beginning of the period. For example, if they are semiannual payments, they would be January 1 and July 1. In this case we use a “1”.

Returning to the example of the $100,000 loan, we know that the payments are at the end of the semester, so we indicate to the PAYMENT function that the type is “0”, that is, at the end of the period:

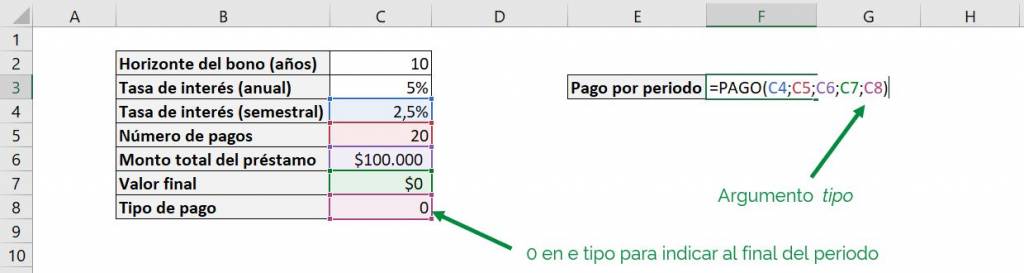
With what we obtain:

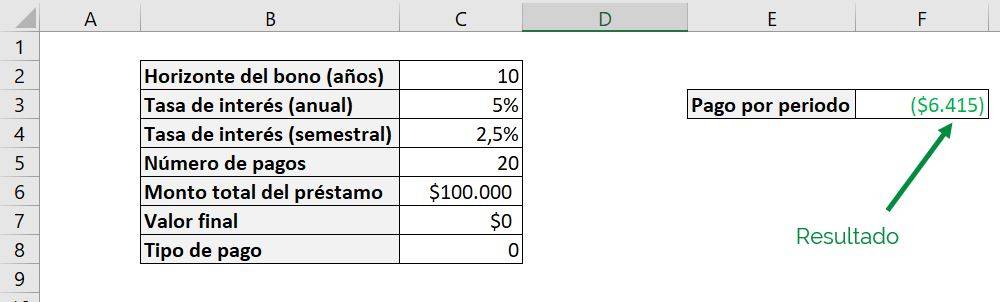
We can see that it corresponds to the same result of Step 3 of $6.415 since, as we said before, by omitting the argument guy The PAYMENT function assumes that payments are at the end of the period, similar to entering “0”. On the other hand, if we now say that the payments are at the beginning:

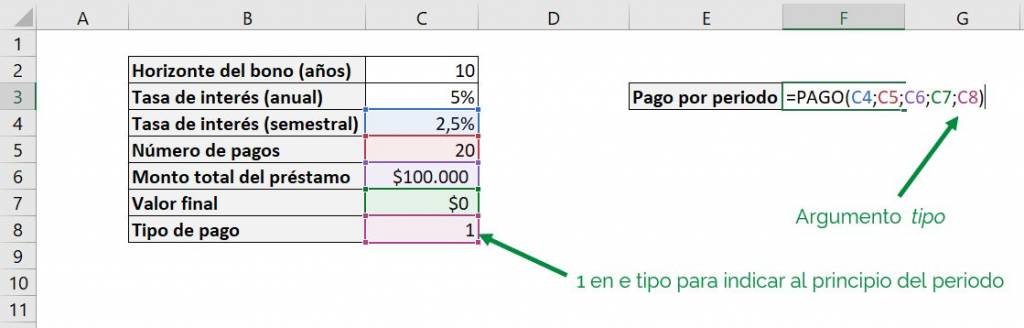
With what we obtain:

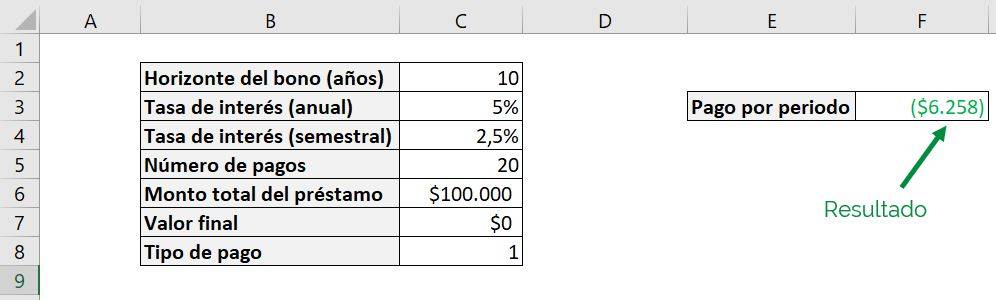
We can see that now the semiannual payment falls to $6.258. The payment delivered by the PAYMENT formula is less because since the payments are up front, there is less time over which to pay interest.