CAGR: Become a financial expert

Know how to find the compound annual growth rate (CAGR) of an investment, income, returns, among others, is the basis for better understanding interest rates. In this article you will quickly learn how to calculate CAGR through two methods.

Key information:

To calculate the CAGR in a period of time there is no function in Excel, due to this, we must calculate it through different methods such as the Excel RRI function or the general CAGR formula.

What is CAGR?

The compound annual growth rate (CAGR) measures the rate of return on an investment over a period of time. It is also known as a “smoothed” rate of return, as it measures the growth of an investment at a constant annual rate.

Excel does not have a function called CAGR, therefore, to calculate it we can use the Excel RRI function or use the manual CAGR formula, let's look at each case.

Tip Ninja: We must know that CAGR is not the average of interest rates from one year to the next, in fact, they deliver very different results. If you want to learn how to calculate the annual interest rate of an investment, we recommend visiting TASA.

Way 1: RRI to calculate CAGR

This way consists of using the Excel RRI function. This function provides the equivalent interest rate for the growth of an investment for a given period of time.

Tip Ninja: If you want to learn more about this feature, we recommend visiting RRI.

Let's remember that this function has three arguments, these are:

nper: Number of investment periods.
goes: Current value of the investment.
vf: Future value of the investment.

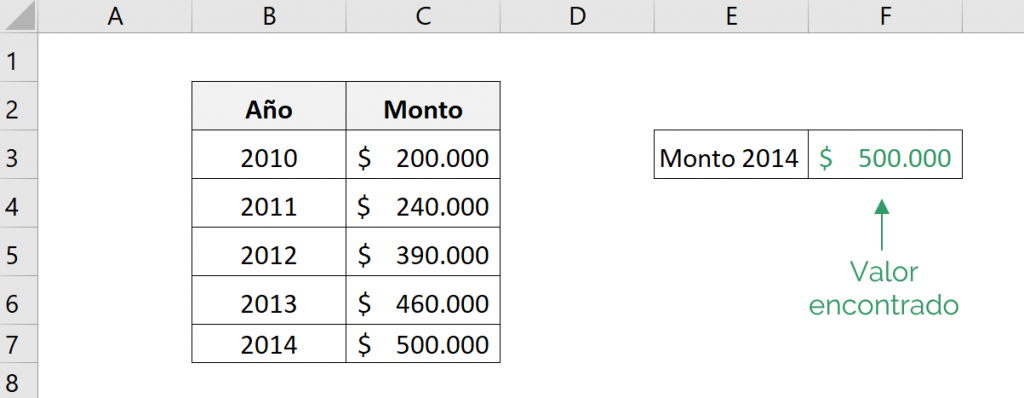
To better understand the logic of CAGR let's look at a simple example. Let's assume the following returns generated by an investment over a period of 5 years.

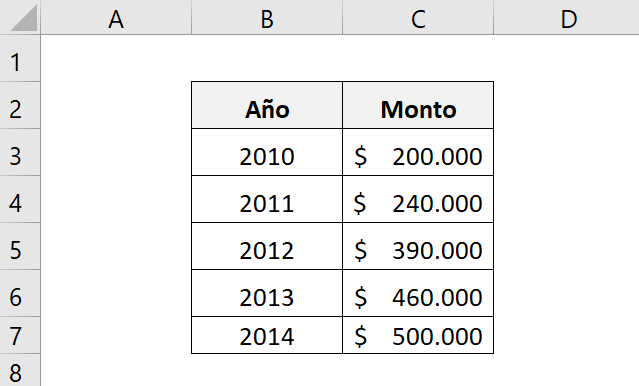
We want to know the constant annual interest rate for these 5 years, that is, we want to find an interest rate that is the same for the five years, reaching the same final amount from an initial amount.

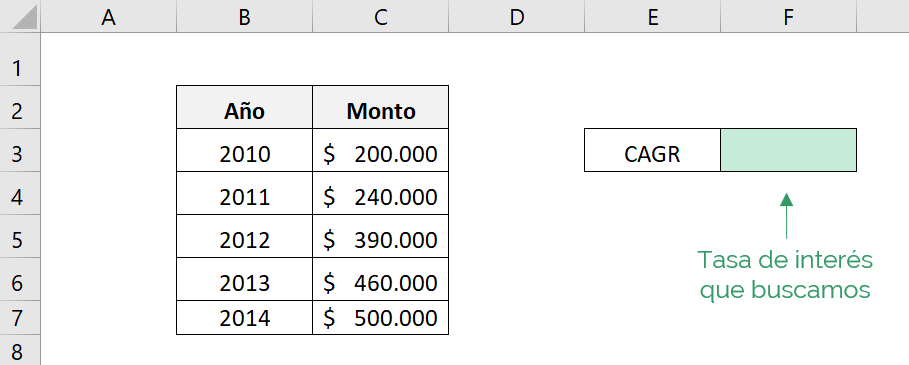
As we can see, the investment was maintained for 5 years, therefore, the RRI function does not care what those years were, but rather the number of years that have passed. Therefore, for this function the current value “goes” corresponds to the initial amount of the investment, in the example: $200,000 and the final value “vf” corresponds to the final amount of the investment, in the example: $500,000.

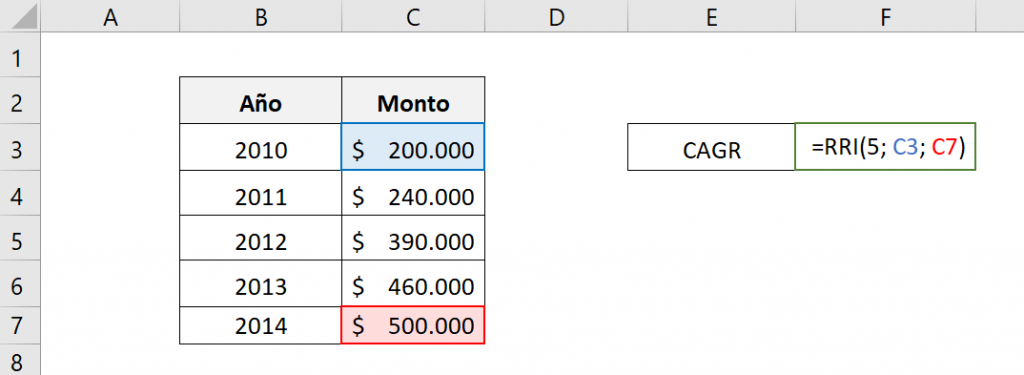
The elements of the function are:

nper: 5
goes: C3
vf: C7

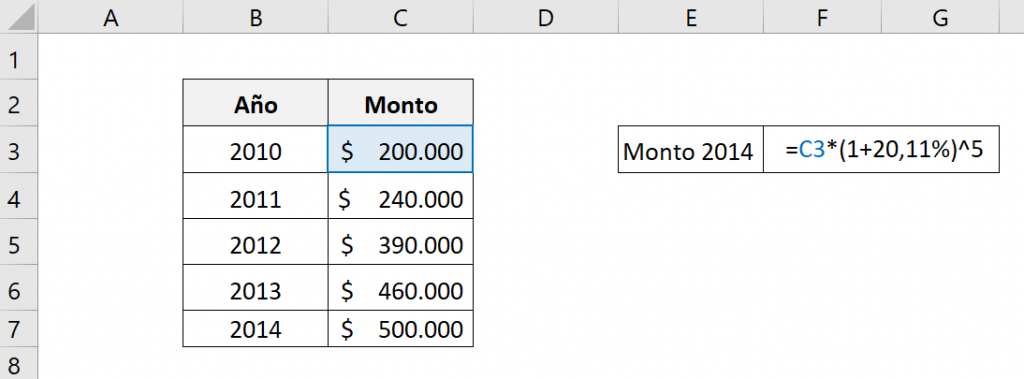
That is, the RRI function is:

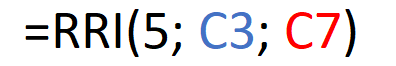
The result we will obtain will be:

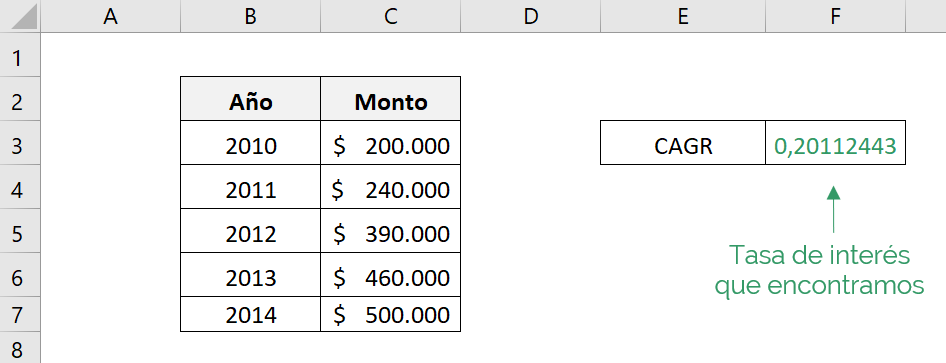
Therefore, to obtain $500,000 from an investment of $200,000 there must be a compound annual rate of approximately 20,11%.

Tip Ninja: If using the RRI function to obtain the CAGR resulted in an error, you can use the IF.ERROR or IF.ND functions to control the errors.

What CAGR tries to say, in mathematical terms, is that if we multiply $200,000 five times by (1+.20.11%), corresponding to the 5 years, we will obtain $500,000.

To understand it better, let's calculate it. We want to know the amount we would obtain in 5 years, starting today, with an initial investment of $200,000 and with a CAGR of 20,11%, that is, we are looking for the amount for the year 2014.

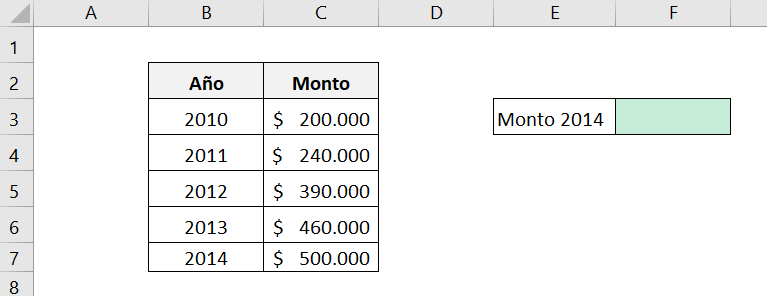
To do this, we must multiply the initial amount by (1+r) corresponding to each year, where r is the constant annual interest rate, that is, we must multiply $200,000 by five times (1+20,11%).

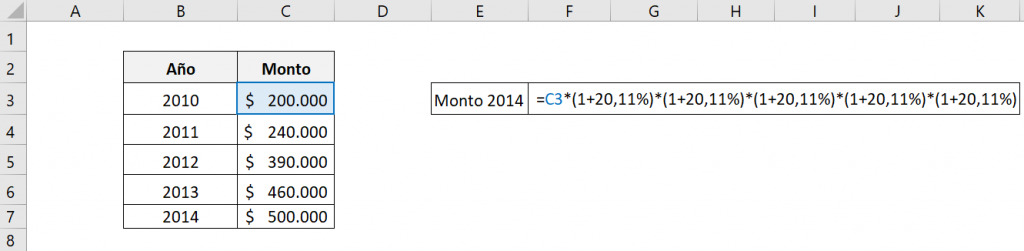
Therefore, the equation used is:

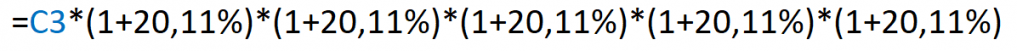
The result we obtain will be:

We can summarize this equation using powers, as follows:

Therefore, the equation used is:

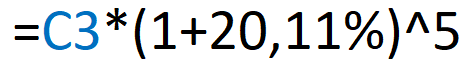
The result we obtain is the same, an amount of $500,000.

Tip Ninja: Using CAGR we cannot obtain the amount for each year, only the final or initial one. For example, we cannot know the exact amount for the year 2012, since if we multiply $200,000 by (1+20,11%)^2, we obtain approximately 289,000, instead of obtaining the 390,000 corresponding to that year. This happens because from one year to the next there is a different interest rate than the CAGR.

Way 2: Manual formula to get CAGR

The formula used to obtain the CAGR of an investment is the following:

But how do we obtain this formula?

Let's remember the formula that we obtained in the previous example, where we look for the final amount based on an investment made for five years:

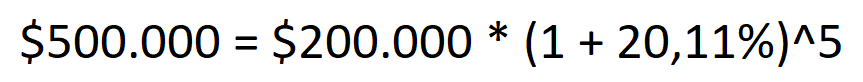
Let's replace these numbers with the ones that mean:

$500,000: This is the final amount we are looking for.
$200,000: This is the initial amount we invested.
20.11%: It is the CAGR.
5: It is the number of years that we invested the initial amount, we call the number of years by “n”.

From this, we obtain the following formula:

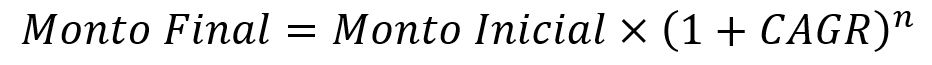
As we are looking for a formula for CAGR we must solve “CAGR” of the equation by following the following steps:

To pass the "Starting amount” dividing to the left side of the equation:

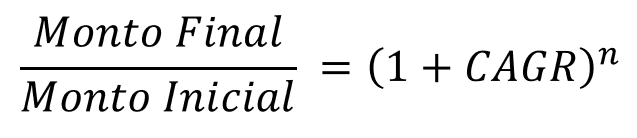
To remove the “n” on the right side of the equation, we must add an nth root, that is, raise to (1/n):

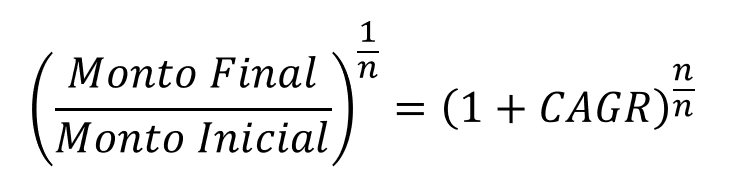
In this way, the right side of the equation will be raised to 1, since (n/n)=1.

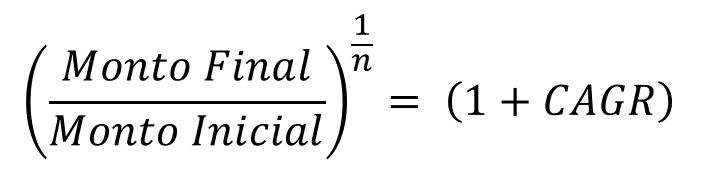
Now, for CAGR to be the only term on the right side of the equation, we must subtract the 1 to the left side, obtaining the CAGR formula:

Let's go back to the previous example and calculate the CAGR through the formula. Let's remember the investment amounts.

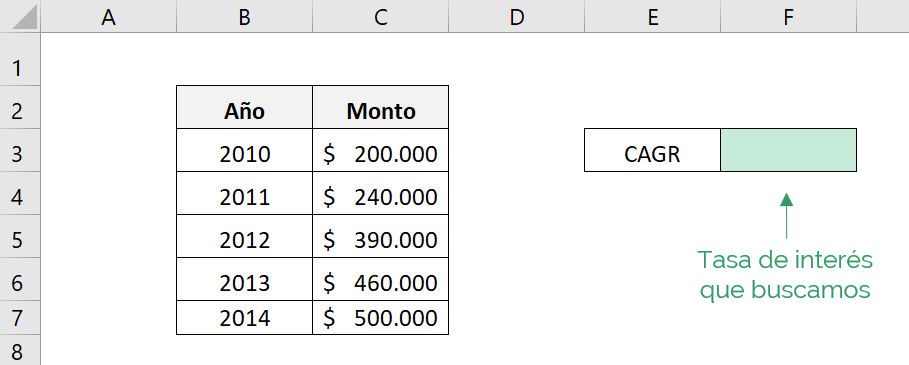
First, let's identify the values we need to plug into the equation.

Starting amount: $200.000
Final Amount: $500.000
N: 5

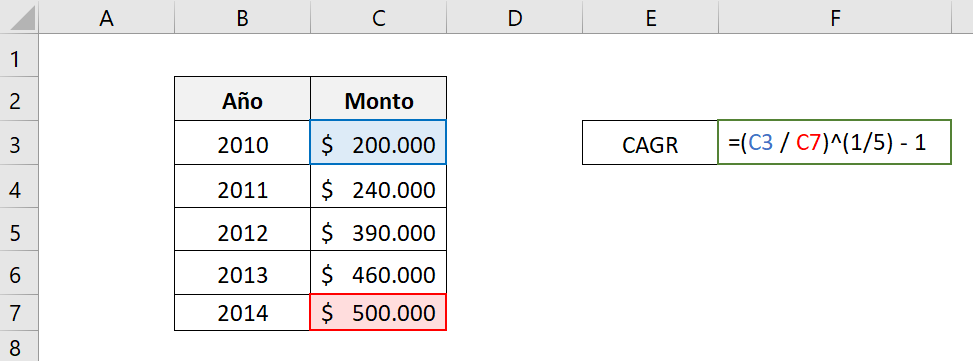
We can see that instead of writing the initial and final amounts, we select the cells that contain them, that is, the formula is:

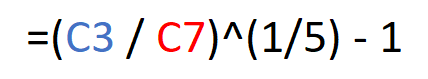
We obtain the following result:

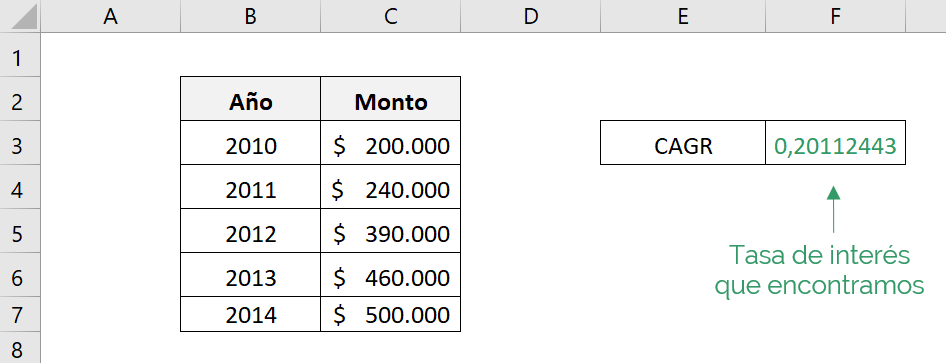
That is, the CAGR is approximately 20.11%.

We can see that we got the same CAGR for both forms used, the RRI function and the manual CAGR formula.

In conclusion, if you want to calculate the CAGR of an investment in a certain period, you must divide the final amount by the initial amount, then raise it to 1 divided by the number of periods and finally, subtract 1.