Prueba t Excel: aprende cómo aplicarla y prueba tu destreza

1. Lo básico de prueba t Excel

¿Qué es la prueba t?

La prueba T-Student es un tipo de estadística deductiva. Se usa para analizar el comportamiento de dos muestras diferentes.

¿Para qué sirve la prueba t?

T test Excel se usa para analizar si hay una diferencia significativa entre las medias de dos muestras diferentes.

Recordemos un par de conceptos claves.

Prueba de hipótesis: Es una regla para aceptar o rechazar una afirmación. Para esto, analiza dos hipótesis de una población que se oponen: la hipótesis nula y la hipótesis de alternativa.

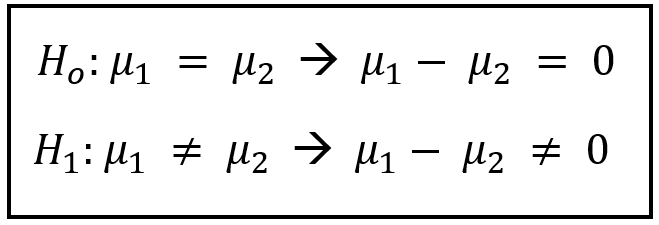
Hipótesis nula (H0): conjetura de un parámetro que se quiere probar. Generalmente la hipótesis nula consiste en la igualdad de un parámetro en las dos muestras (ausencia de diferencia o efecto). En el caso de la prueba t Excel es la igualdad de las medias en dos muestras.

Hipótesis alternativa (H1): conjetura de un parámetro que se cumple si se rechaza la hipótesis nula. Generalmente consiste en la diferencia de un parámetro en las dos muestras. Para la prueba t Excel es que sí existe una diferencia en las medias de dos muestras.

Podemos verlo en la imagen de la siguiente manera:

¿Cuándo se rechaza la hipótesis nula en una prueba t Excel (H0)?

1. Si el valor absoluto t–Student calculado (estadístico t) es mayor al t tabulado (valor crítico de t dos colas).
2. Si el p – valor es menor al alfa de significancia de la prueba t–Student. El valor p es una medida de evidencia en contra de H0. Si se cumple lo anterior, se tiene suficiente evidencia para rechazar H0. Si no se cumple, es estadísticamente no significativo, y por lo tanto no se puede rechazar H0.

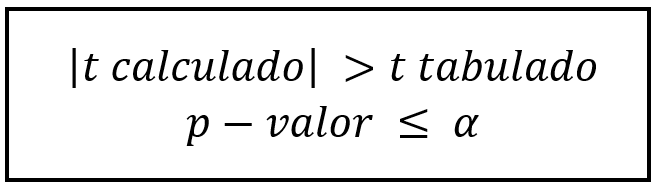
Atención Ninja:

La prueba t de Excel trabaja al 95% de confianza para realizar sus análisis, de manera predeterminada. De esta manera el alfa de una prueba t de Excel es 0,05.

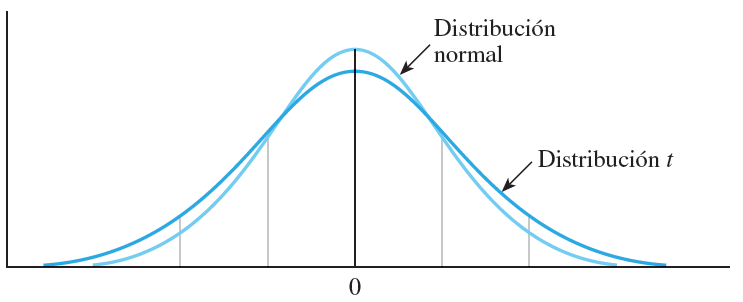
Se puede realizar la prueba t en Excel de tres maneras diferentes:

1. Prueba t para dos muestras suponiendo varianzas iguales.
2. Prueba t para dos muestras suponiendo varianzas desiguales.
3. Prueba t de dos muestras emparejadas.

La diferencia se debe a las varianzas. Para aplicar una u otra opción en una prueba t en Excel, debemos saber cómo se comportan las varianzas de las muestras. Para esto debemos realizar una prueba Fisher en Excel. Con la prueba f se determina la igualdad de las varianzas de dos muestras (hipótesis nula).

Por lo tanto, una vez realizada la prueba f, podremos saber el comportamiento de las varianzas y cuál de los métodos de prueba t implementar.

Para aplicar la prueba t y la prueba f, debemos cargar el complemento de “Análisis de Datos”.

2. Complemento “Análisis de Datos” para prueba t en Excel

La herramienta de “Análisis de Datos” permite realizar distintos análisis estadísticos, financieros y técnicos a través de diferentes instrumentos.

¿Cómo se carga?

Vamos a “Archivo”, damos clic en “Opciones”. Luego seleccionamos “Complementos”, damos clic en “Herramientas para análisis”, y apretamos la tecla “Ir”, como muestra la imagen.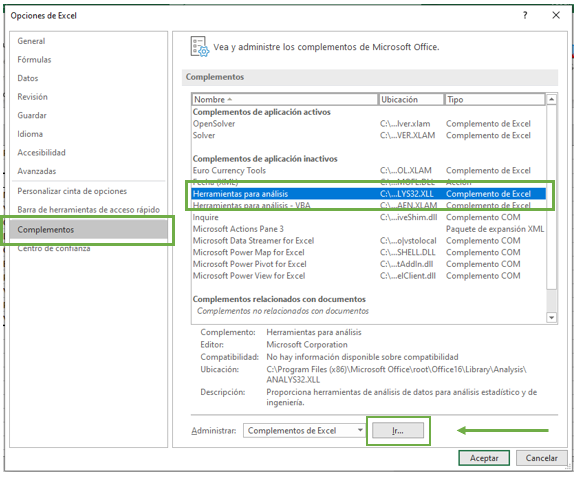Damos clic en “Herramientas para análisis”, y apretamos “Aceptar”.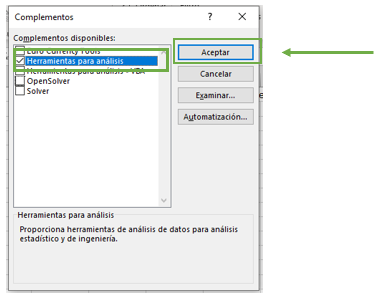

Si vamos ahora a “Datos”, en la parte de “Análisis”, aparece el complemento “Análisis de Datos”.

3. Prueba t Excel para dos muestras suponiendo varianzas desiguales

La prueba t Excel permite comparar la media de dos muestras con varianzas distintas.

Este post podría serte útil si te interesa saber cómo calcular la desviación estándar en Excel.

Imaginemos el siguiente ejemplo donde tenemos las notas de dos cursos, como muestra la tabla a continuación.

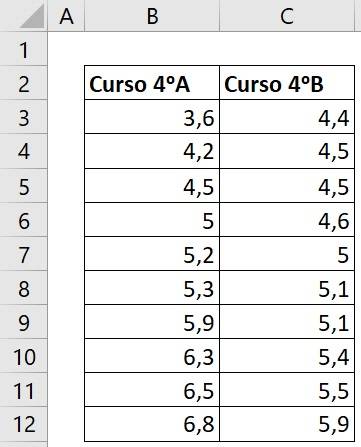
El primer paso para realizar una prueba t Excel, es saber si las varianzas de estos dos cursos son iguales. Para ello debemos realizar una prueba f, siendo la hipótesis nula y la hipótesis alternativa las que se muestran en la imagen a continuación:

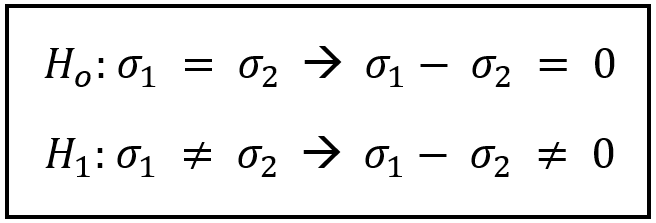
¿Cómo realizamos la prueba f Excel?

Vamos a “Datos”, en “Análisis” apretamos “Análisis de Datos”.

Apretamos “Prueba F para varianzas de dos muestras”.

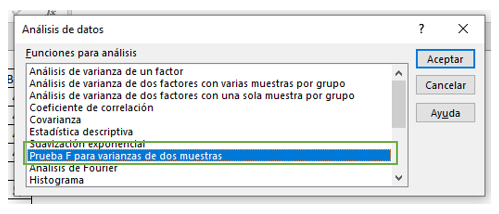
Nos aparece el siguiente recuadro de la imagen que debemos rellenar.

1. En el rango 1 seleccionamos los datos de la muestra 1, en este caso las notas del curso 4A con el nombre de la muestra.
2. En el rango 2 seleccionamos los datos de la muestra 2, es decir, las notas del curso 4B con el nombre de la muestra.
3. Damos clic en “Rótulos”, ya que hemos seleccionado el nombre de cada muestra.
4. El alfa predeterminado de Excel es 0,05, el cual podemos cambiar si queremos. En este caso lo dejaremos así.
5. Finalmente seleccionamos el lugar donde queremos que aparezca la tabla en la hoja actual. También Excel nos da la opción de ponerla en una hoja nueva, o un libro nuevo.

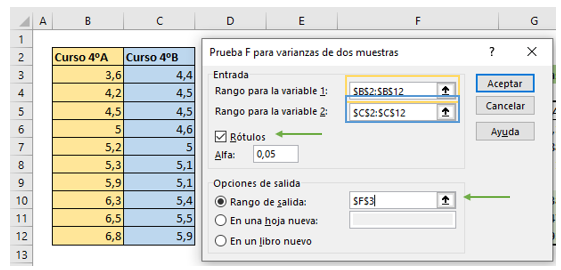
De esta forma, nos entrega una tabla con el siguiente análisis.

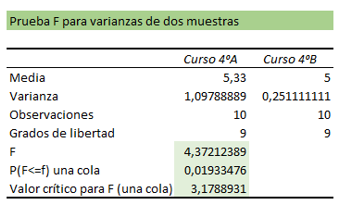
Recordemos que la hipótesis nula en una prueba Fisher se rechaza si se cumple alguna de estas dos condiciones:

1. 0,05 > 0,01933476
2. 4,37212389 > 3,1788931

Vemos que ambas se cumplen, por lo tanto, se rechaza la hipótesis nula y las varianzas de notas de los dos cursos no son iguales.

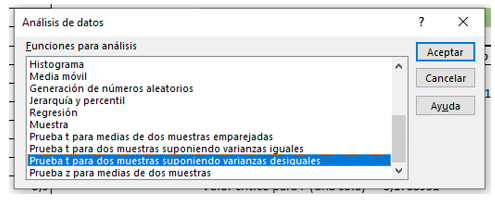
Ahora que sabemos esto, podemos realizar la prueba t. Vamos al igual que antes a “Análisis de Datos”, y ahora seleccionamos “Prueba t para dos muestras suponiendo varianzas desiguales”.

Nos aparece un recuadro para la prueba t muy parecido al anterior, el cual debemos rellenar de forma similar.

1. En el rango 1 seleccionamos los datos de la muestra 1, es decir, las notas del curso 4A con el nombre de la muestra.
2. En el rango 2 seleccionamos los datos de la muestra 2, en este caso las notas del curso 4B con el nombre de la muestra.
3. Damos clic en “Rótulos”, ya que hemos seleccionado el nombre de cada muestra.
4. El alfa predeterminado de Excel es 0,05, el cual podemos cambiar si queremos. En este caso también lo dejaremos así.
5. Finalmente seleccionamos el lugar donde queremos que aparezca la tabla en la hoja actual. También Excel nos da la opción de ponerla en una hoja nueva, o un libro nuevo.

La diferencia será que debemos poner un cero en “Diferencia hipotética entre las medias”, ya que esa es nuestra hipótesis nula de nuestra prueba t, que las medias de los dos cursos son iguales (que la diferencia entre ellas es cero).

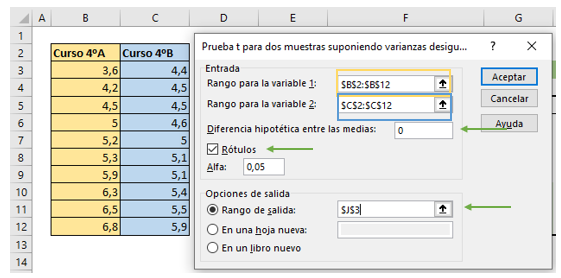
Nos aparece el siguiente recuadro para la prueba t Excel:

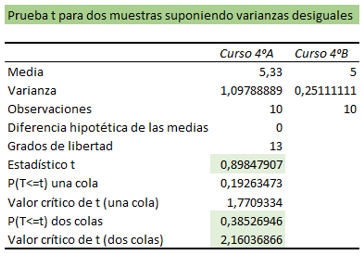
A partir de esta tabla podemos probar hipótesis nula de nuestra prueba t Excel, la cual se rechaza si se cumple alguna de estas dos condiciones:

1. 0,05 > 0,38526946
2. 2,16036866 < 0,89847907

Vemos que ninguna de las dos se cumple, por lo tanto, no hay evidencia significativa para decir que las medias de las notas de los dos cursos son diferentes. La hipótesis nula de nuestra prueba t Excel no se rechaza.

4. Prueba t Excel para dos muestras suponiendo varianzas iguales

Ahora supongamos que se hace la comparación de notas del curso 4 A con el 4 C, como muestra la tabla.

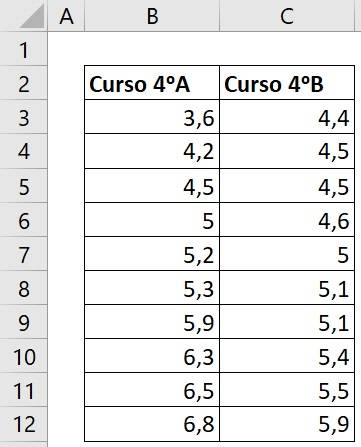
Debemos ver el comportamiento de las varianzas de estas dos muestras para saber qué prueba t Excel vamos a realizar.

Vamos a “Análisis de datos” y seleccionamos “Prueba F para varianzas de dos muestras” al igual que antes.

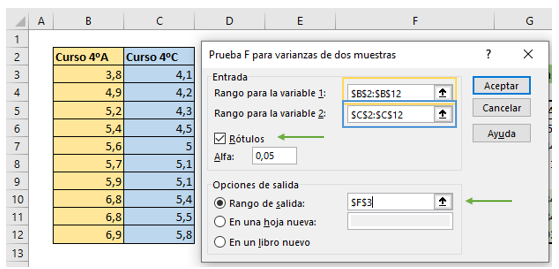
Rellenamos los datos al igual que en el ejemplo anterior, como muestra la imagen.

Nos aparece el siguiente cuadro resumen.

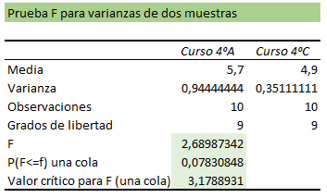
La hipótesis nula en una prueba Fisher se rechaza si se cumple alguna de estas dos condiciones:

1. 0,05 > 0,07830848
2. 2,68987342 > 3,1788931

Vemos que no se cumple lo anterior, y por lo tanto no se rechaza la hipótesis nula, ya que no hay evidencia significativa para decir que las varianzas de las notas de los dos cursos son diferentes. Se asume varianzas iguales de los dos cursos.

De esta forma vamos a “Análisis de Datos” y seleccionamos “Prueba t para dos muestras suponiendo varianzas iguales”.

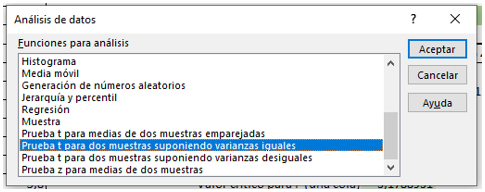
Rellenamos los datos de nuestra prueba t Excel al igual que antes, como muestra la imagen.

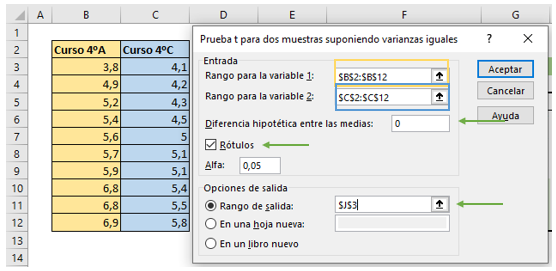
Nos aparece el siguiente cuadro resumen de nuestra prueba t Excel.

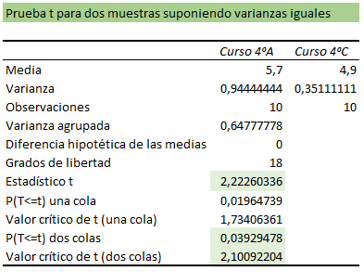
Con esta tabla podemos probar la hipótesis nula de nuestra prueba t Excel, la cual se rechaza si se cumple alguna de estas dos condiciones:

1. 0,05 > 0,03929478
2. 2,10092204 < 2,22260336

Vemos que se cumple lo anterior, por lo tanto, se rechaza la hipótesis nula de nuestra prueba t Excel, es decir, las medias de las notas de los dos cursos son distintas.

5. Prueba t Excel para medias de dos muestras emparejadas

Esta prueba t Excel se ocupa cuando no hay independencia total entre las muestras. Para esta prueba las variables deben tener el mismo número de observaciones.

Se realiza de manera similar que las dos pruebas descritas anteriormente, pero esta vez marcaremos la opción “Prueba t para medias de dos muestras emparejadas”, como muestra la imagen sin necesidad de hacer una prueba F Excel anteriormente.